Precision & Recall
Precision 은 모델의 예측 값 중, 실제 값과 같은 데이터의 비율을 말하고,
Recall 은 실제 값 중, 모델의 예측 값과 같은 데이터의 비율을 말한다.
다시 정리하면,
예측해야할 값의 클래스가 A, B, C 가 있다고 할 때,
Precision = (예측 데이터 중, 실제 클래스 A 인 데이터의 수) / (클래스 A 로 예측된 값들의 데이터 수)
Recall = (실제 데이터 중, 클래스 A 로 예측된 값들의 데이터 수) / (실제 클래스 A 인 데이터의 수)
일반적으로 각 클래스 A, B, C 에 대한 각각의 성능 지표를 구한 뒤, 평균을 내어 하나의 지표로 통합하여 표현한다. 평균 외에 다른 방법도 있긴 하다.
이 두 값 모두 0~1 사이의 값을 가지며 1로 갈수록 좋다.

위 그림을 예로 들어보면,
Cat 에 대한 Precision 은 4 / (4+6+3) 이고, Recall 은 4 / (4+1+1) 이다.
Precision 과 Recall 중 무엇을 사용할지는 상황에 따라 다르다.
예를 들어, 암 환자를 진단하는 경우를 생각해보면, Precision 과 Recall 은 다음과 같이 생각해볼 수 있다.
- Precision : 암 환자라 예측한 수 중 실제 암환자인 비율
- Recall : 실제 암환자 중, 예측한 암환자의 비율
이 경우 Recall 을 사용해야 한다.
암 환자가 100명이 있다고 하자. 이 중 내가 만든 모델이 30명을 암환자라고 예측했고, 실제 이 30명은 암환자 였다고 하자.
Precision 값은 30 / 30 = 1이 되고, 이 모델은 매우 좋은 성능을 지니는 것 처럼 보인다.
하지만 실제 암 환자임에도 암 환자라고 진단받지 못한 70명에게는 굉장히 치명적이다.
정상 환자를 암 환자로 잘못진단 하는 것 보다, 암 환자를 정상 환자로 진단하는 것이 상식적으로 더 위험하기 때문이다.
Recall 로 계산해보면, 30 / 100 이 되고, 이 모델은 매우 좋지 않은 성능을 지니는 것을 알 수 있다.
일반적으로, Precision 과 Recall 은 Trade-off 관계에 있다.
따라서, 위와 같이 어떤 지표를 사용할지 확실한 경우가 아니면, 한 값만 극단적이지 않고 두 값 모두 적절히 높은 것이 좋은 성능을 나타낸다 하겠다.
F1-score
F1 score 는 Precision 과 Recall 두 값 모두 고려하기 위한 지표로, 이 두 값을 조화평균을 내어 계산한다.
0~1 사이의 값을 가지며 1로 갈수록 좋다.
클래스 데이터가 불균형할 때 사용하기 좋다.
Accuracy
Accuracy 는 전체 데이터 중, 실제 정답과 동일한 데이터 수의 비율을 말한다.
즉, Accuracy = (실제 데이터 = 예측 데이터 인 데이터 수) / (전체 데이터 수)
가장 직관적이고 사용하기 편하지만,
클래스 데이터가 불균형할 때 해석의 왜곡을 불러온다.
예를 들어, 전체 데이터 100가 있고 이 중 A 클래스가 90개 , B클래스가 10개가 있다고 하자.
만약 내가 만든 모델이 A 클래스는 100개, B 클래스는 0개라고 예측해도 accuracy 는 90%가 된다.
90% 라는 수치만 보면 잘 예측하는 모델이라 생각할 수 있는데, 사실 예측 값을 놓고보면 전혀 아닌 것이다.
따라서, 클래스 데이터가 어느 정도 균형구조일 때만 사용하는게 일반적이다.
Confusion Matrix
Confusion Matrix 는 성능 평가지표 그 자체는 아니지만, 위에서 설명한 지표들을 하나의 Matrix 로 설명할 수 있다.
먼저, Confusion Matrix 는 이진 분류 상황만을 가정한다.
다음과 같이 예측 값-실제 값을 비교한 테이블, Confusion Matrix 라 불리는 테이블을 만들 수 있다.

예측 값과 실제 값을 비교하면 다음과 같이 4가지 경우의 수가 나온다.
- TP (True Positive) : 맞춘 경우. 실제 값이 1이고, 예측 값도 1인 경우.
- FN (False Negative) : 틀린 경우. 실제 값이 1인데, 예측 값은 0인 경우.
- FP (False Positive : 틀린 경우. 실제 값이 0인데, 예측 값은 1인 경우.
- TN (True Negatives) : 맞춘 경우. 실제 값이 0이고, 예측 값도 0인 경우.
TP 에서 앞의 T 는 실제 값 == 예측 값인 경우를 의미하고, P 는 예측 값이 1인 경우를 의미한다.
맞췄는가? T 예측값은? P. 이런 순서로 이해하면 보기가 쉽다.
위에서 이야기한 3가지 지표는 이제 다음과 같이 이해해볼 수 있다.
- Accuracy
- 전체 케이스 중, 맞춘 케이스의 비율
- (TP + TN) / (TP + FN + FP + TN)
- Precision
- 모델이 1이라고 예측한 케이스 중, 실제 값이 1인 케이스의 비율
- TP / (TP + FP)
- Recall
- 실제 값이 1인 케이스 중, 모델이 1이라고 예측한 케이스의 비율
- TP / (TP + FN)
ROC-AUC score
ROC-AUC 는 좀 더 섬세한 설명이 필요하다.
StatQuest with Josh Starmer 의 영상을 참고하여 적어둔다.
먼저, ROC-AUC score 를 사용하기 위해서는 우리가 예측한 값은 0~1 사이에 있어야 한다.
즉 이전에는 단순히 0과 1로만 예측했다면 이제는 0.33 이라든가 0.56 과 같은 값도 가능하다는 말이다.
여기서는 예를 들기 위해, 몸무게로 비만인지 아닌지를 예측해보는 문제를 풀어보자.
예측 모델을 Logistic Regression 을 사용한다고 하자.
Logistic Regression 은 0~1 사이의 값으로 예측한다.

Logistic Regression 모델을 훈련시켜 다음과 같은 함수를 얻었다.

각 데이터는 Logistic Regression 함수 식에 입력되어 0과 1사이의 값 (그래프에서 Is Not Obese 는 0 Is Obese 는 1이다) 으로 예측될 것이다.
이제 적절한 threshold 를 두어, 이렇게 0~1로 나온 값들을 0과 1로 분류해보자.
먼저 0.5를 threshold 로 두면 다음과 같이 된다.
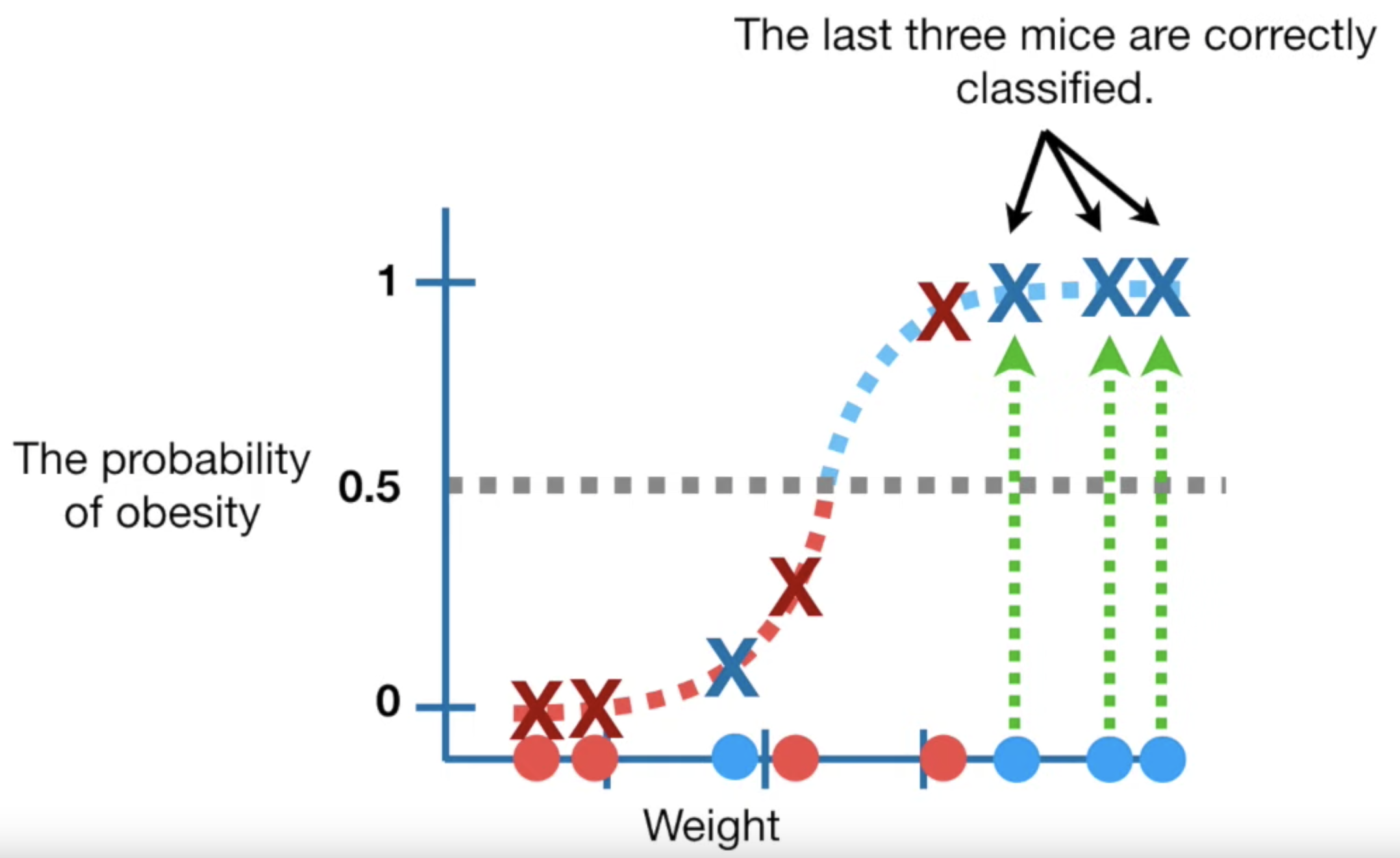
잘 분류가 된 것도 있고, 잘 분류가 안된 것도 있다.
위 그래프에서는 2개의 데이터만 잘 분류가 안되었다.
(1인데 0으로 분류된 데이터 1개, 0인데 1로 분류된 데이터 1개)
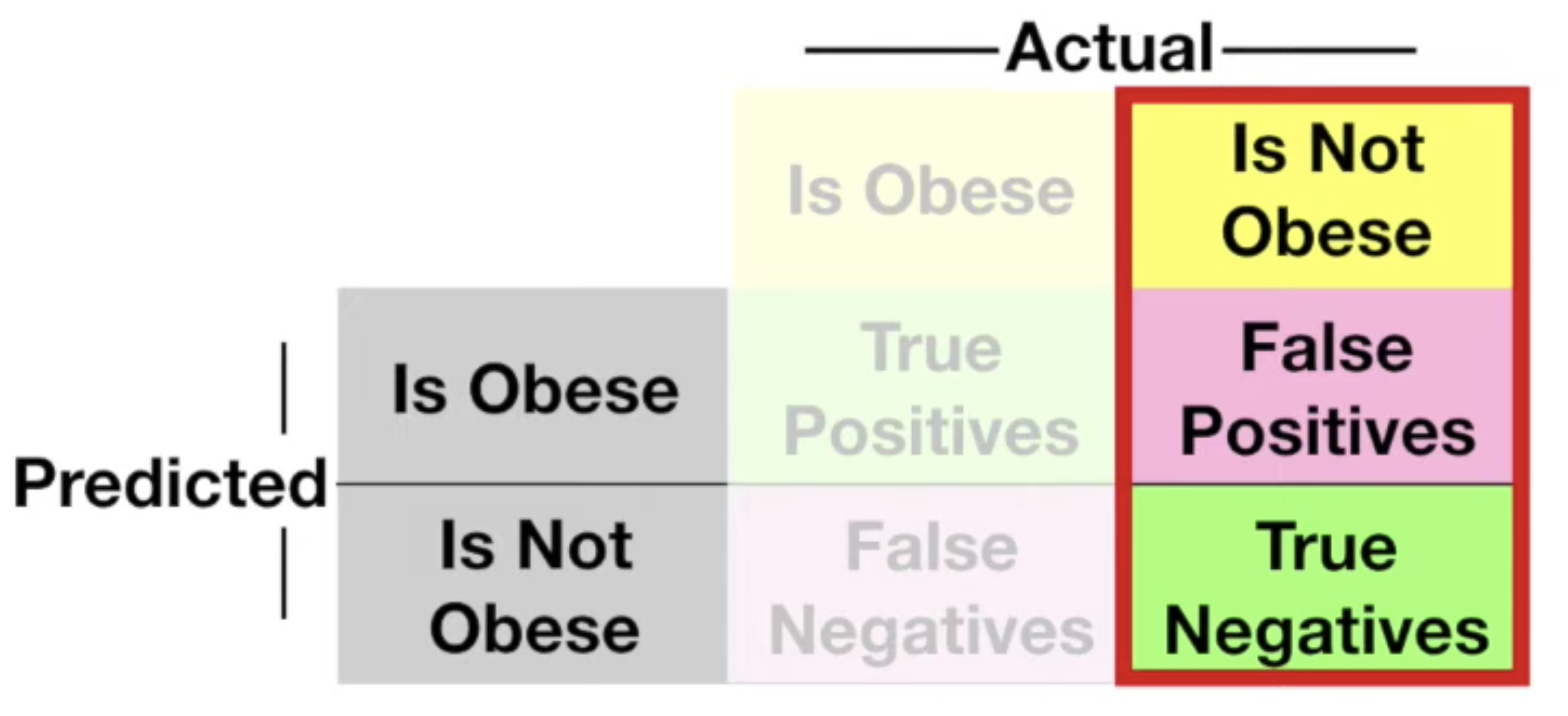
이제 이를 Confusion Matrix 로 보면 다음과 같다.

이제 Confusion Matrix 에서 우리가 관심있는 것만 보기로한다.
우리는 TPR (True Postivie Rate) 과 FPR (False Positive Rate) 에만 관심을 가질 것이다.
TPR 은 다음과 같이 정의된다.
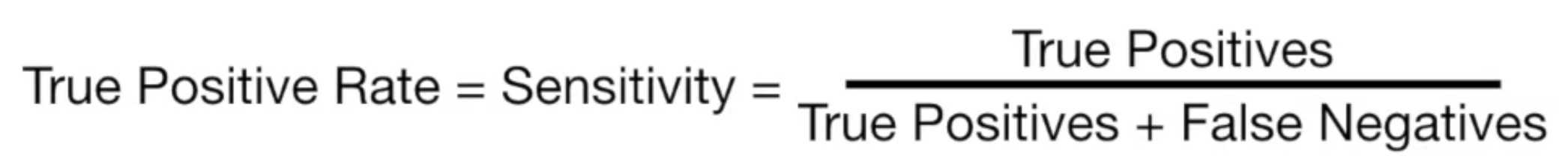

실제로 1인 것 중 내가 예측한 값이 1인 비율이며, Recall 하고 동일한 값이다.
즉 내가 잘 예측한 경우다. 이 값은 높을수록 좋다.
FPR 은 다음과 같이 정의된다.
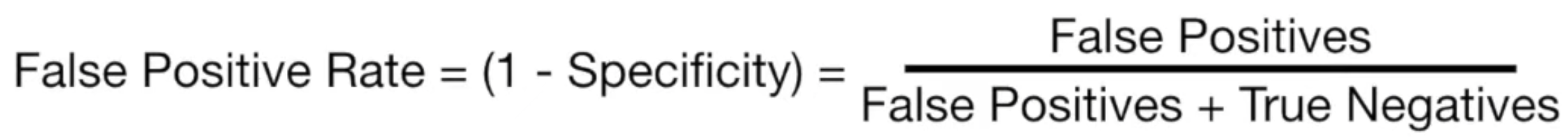
실제로는 0인 것중, 내가 예측한 것이 1인 비율이다.
즉, 내가 잘 못 예측한 경우다. 이 값은 낮을수록 좋다.
지금까지 한걸 생각해보자.
훈련시켜놓은 모델을 가지고,
- 하나의 threshold = 0.5를 가지고
- TPR 과 FPR 을 계산할 수 있다.
이제 다음과 같은 그래프를 생각하고, Threshold 를 0부터 1까지 옮겨보며 TPR과 FPR 을 계산해보자.
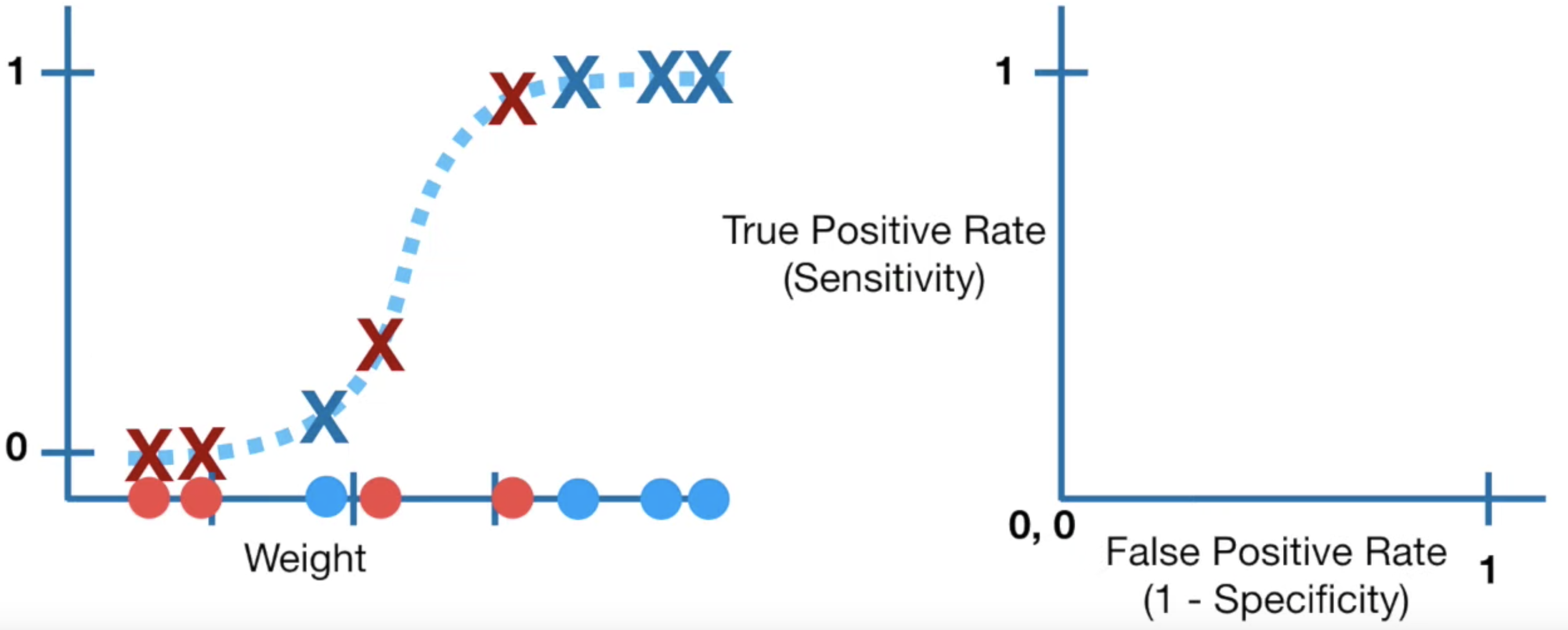
맨 처음 Threshold 가 0인 경우를 보자.
이 경우에도 마찬가지로 Confusion Matrix 를 그려볼 수 있고, 여기에서 TPR 과 FPR 값을 계산할 수 있다.
Threshold 가 0인 경우, TPR 은 1 FPR 은 1 이 된다.
이를 오른쪽 그래프에 점으로 찍으면 다음과 같다.

생각해보자. 방금은 TPR = FPR = 1 이었다.
TPR 과 FPR 이 같다는게 무슨 의미일까?
TPR 과 FPR 의 정의를 생각해보면, 잘 맞추는 비율, 잘 못 맞추는 비율 정도로 생각해볼 수 있는데,
TPR = FPR 이라는건, 내가 예측한 값 중, 절반은 맞고 절반은 틀리다는 것이다.
그리고 Threshold 를 0부터 1까지 옮기면서, TPR = FPR 이 되는 경우는 앞으로 위 그래프에서 초록색 점선 위로 등장할 것이다.
이제 다시 Threshold 를 0에서 0.1, 0.2 ... 1까지 하나씩 옮겨보며 TPR, FPR 을 계산하고 이를 그래프에 점으로 찍어보자.

이렇게 0부터 1까지 Threshold 를 옮기면 무수히 많은 점이 찍힐 것이다.
이렇게 찍힌 점들을 쭉 연결하고, x축과의 넓이를 구하면 다음과 같이 빨간색으로 표시할 수 있다.

먼저 이렇게 점들을 연결한 곡선을 ROC 커브 (Receiver Operating Characteristic) 라고 한다.
그리고 그 곡선 아래의 넓이를 AUC (Area Under Curve) 라고 하며, 이게 이 모델의 성능지표가 된다.
이 넓이 값을 구해보니 0.9 였다.
이 값이 왜 모델의 성능 지표인가?
우리가 지금까지 사용한 모델말고, 다른 모델로 같은 문제를 예측했다고 해보자.
그리고 이 다른 모델 역시 같은 과정을 통해 AUC 를 나타낼 수 있다.
여기서는 파란색으로 표시하였다.

딱 봐도 면적이 빨간색 보다 작다.
이게 무엇을 의미하는 걸까?
x 축과 y 축을 다시 살펴보자.
y 축은 TPR 을 나타낸다. 즉 TPR 높을수록 모델은 잘 예측하고 있는 것이고, TPR 이 높을수록 모델의 AUC 가 넓어진다.
즉, 우리는 이 넓이 값, AUC 의 값으로 빨간색을 그려낸 모델이 파란색을 그려낸 모델보다 더 잘 예측하는 모델임을 알 수 있다.
정리해보면, ROC AUC score 는 Threshold 를 0부터 1까지 옮기며 곡선을 그리고 그 곡선 아래의 넓이를 구한 값이라 할 수 있겠다.
'데이터와 함께 탱고를 > 머신러닝' 카테고리의 다른 글
| 회귀 모델에 대한 성능 평가 지표들 (0) | 2020.02.06 |
|---|---|
| Word2Vec 과 Doc2Vec (0) | 2020.01.29 |
| 코사인 vs 유클리디안 유사도, 케이스로 이해하기 (0) | 2019.12.11 |
| Catboost 주요 개념과 특징 이해하기 (7) | 2019.10.23 |
| Categorical Value Encoding 과 Mean Encoding (3) | 2019.09.07 |
 하나씩 점을 찍어 나가며
하나씩 점을 찍어 나가며

