가설 검정을 배우는 이유는, 실제로 써먹기 위함이고, 써먹으려면 실제 현실의 여러 상황에 맞게 배워야 한다.
고로, 현실의 여러 상황들을 정의하고 분류한 뒤, 각 상황에 맞는 테스트를 배우는 것이 가설검정의 목표라고 할 수 있겠다.
대부분의 글들과 내용은 Sapientia a Dei님 유튜브 를 참고한다. (매우 잘 설명되어있어서, 금방 볼 수 있다.)
한 집단의 가설검정
이전까지의 가설검정은 하나의 집단, 즉 단일 집단에 대한 가설 검정 내용이었다.
예를 들어, 다음과 같은 상황과 질문이었다.
배터리 A의 수명은 1년이라고 알려져있는데, 최근 소비자들로부터 1년이 아닌 것 같다는 말이 나오고 있다.
이에, 배터리 A 25개를 표본으로 뽑아 조사하였더니, 평균 수명이 11개월이 나왔다고 한다.
어느 의견이 타당한지 유의수준 5% 에서 검정하시오. (모 표준편차는 5개월로 알려져 있다.)
즉, 한 집단의 평균과 다른 숫자를 비교, 검정하는 식이었다.
이제, 단일 집단이 아닌, 두 개 집단에 대해 비교해보려고 한다.
두 집단의 평균차이에 대한 가설 검정
예를 들면, 이런 식이다.
A 대학교의 남자 평균 키는 175cm, B 대학교의 남자 평균 키는 178cm 라고 한다.
이 두 대학의 남자 평균키가 유의미하게 차이가 있는지, 유의수준 5%에서 검정하시오.
두 개의 집단이 등장하고, 집단의 대표값인 평균도 두 개가 나오는 상황이다.
대응 표본과 독립 표본
먼저, '두 집단에 대한 표본' 에 대한 정의가 필요한데, 두 가지 케이스로 갈린다.
- 대응 표본
- 쉽게 말해 같은 집단에 대한 before, after 다.
- 예를 들면, 어떤 집단에 대해, 약물을 투여하기 전과 후를 두 개의 표본으로 보는 것이다.
혹은, 어떤 반의 학생들에게 교재A 로 교육한 후와 교재B 로 교육한 후, 이렇게 두 개의 결과를 비교하는 것이다.
- 독립 표본
- 위 경우를 제외한 우리가 알고있는 일반적인 '두 집단' 비교라고 생각하면 된다.
- 예를 들면, 두 대학의 남자 평균 키 비교라든지,
A사 배터리 수명과 B사 배터리 수명간에 차이가 있는지에 관한 검정을 생각할 수 있다.
각 케이스에 따라 검정방식도 살짝 다르다.
Z-test 와 T-test
한 마디로 표현하자면, 모집단의 분산을 알고있는 경우, Z-test를, 아닌 경우 T-test로 검증한다.
대부분의 현실적인 상황에서는 모집단을 모른다. 즉 우리는 일부 추출한 '표본' 만 안다. 그래서 대부분의 경우 T-test 로 검증한다고 한다. 이는 단일 집단 검정에서도 마찬가지 였다. 이전 포스트를 보자.
일반적으로, 모수의 분산을 아느냐 모르느냐에 따라, Z-test 냐 T-test 냐 로 나뉘고, 정규성을 만족하느냐에 따라 모수검정이냐 비모수검정이냐로 나뉜다.
여하튼, 일반적인 경우 모 분산을 모르므로, T-test 로 진행하고, 여기서는 T-test 로 검정하는 법을 공부한다.
(모 분산을 모르더라도, 표본의 수가 큰 경우, 즉 30 이상인 경우 Z-test 로 검정하기도 한다.)
단일 집단 검정
이전 포스팅 복습내용이라고 생각하면 된다.

대응 표본 검정

기존 t-value 값에서, 검정 통계량 X_bar 가 after의 평균, 모 집단 평균이던 뮤가 before의 평균으로 대체된다고 생각하면 된다.
독립 표본 검정

T-value 값에서 분자는 두 집단의 평균 차이가 되고, 분모는 두 집단의 분산이 된다.
이 때, 표본이 작은 경우, 표본 분산에 대한 신뢰도가 떨어지기 때문에, 두 집단의 표본을 합쳐 도출한 합동분산을 사용하게 된다. s^2 에 대한 식이 합동분산에 대한 식이다. 루트 씌우면 합동 표준편차라고 한다.
아래와 같은꼴로 합동분산을 구할 수도 있다. (주어진게 뭐냐에 따라서 어떤 식을 이용할지가 다르다.)
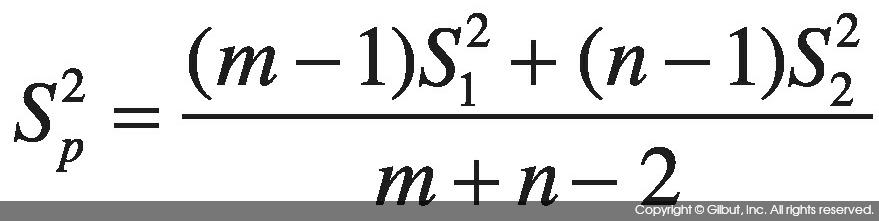
출처 : <https://thebook.io/006723/ch07/07/02/>
문제 예제
출처
대부분 사진에 대한 출처는 *Sapientia a Dei님 유튜브. 3-6 종류별로 알아보자.* 에 있다.
'데이터와 함께 탱고를 > 통계 기초 공부' 카테고리의 다른 글
| 네이버 커넥티드 연수원 간다~! (0) | 2019.06.07 |
|---|---|
| 세 집단 이상의 평균차이에 대한 가설 검정 (0) | 2019.04.23 |
| 가설검정 단계 (지금까지) (0) | 2019.04.18 |
| 표본 분산은 왜 n-1로 나눌까? (0) | 2019.04.18 |
| L1, L2 Regularization (Lasso, Ridge) (0) | 2019.04.09 |
 하나씩 점을 찍어 나가며
하나씩 점을 찍어 나가며


