이 글은 StatQuest with Josh Starmer 의 StatQuest: Random Forest 영상을 보고 정리한 글이다.
모든 사진과 설명에 대한 출처는 여기에 있다.
Bagging 기법의 대표적인 모델인 Random Forest 을 이번 글에 정리해보고자 한다.
Decison Tree 다음에 항상 등장하는 모델로, 일반적으로 DT 보다 더 좋다.
1. 개념
한 마디로 표현하면 다음과 같다.
여러 개의 Boostrapped Dataset 으로 여러 개의 Decison Tree 를 만든 후,
Voting 을 통해 최종 예측값을 출력하는 방법이다.
2. 과정
실제 예를 통해 그 과정을 하나씩 살펴보자.
2.1. Bootstrapped Dataset 만들기
먼저, 다음과 같은 Dataset 이 있다고 하자.

각 row 는 환자 한 명의 데이터이고, Chest Pain, Good Blood Circulation, Blocked Arteries, Weight, Heart Disease 의 유무로 데이터가 구성되어있다. 우리가 만들려고 하는 모델은, 앞의 4가지 Feature (Chest Pain, Good Bllod Circulation, Blocked Arteries, Weight) 로 Heart Disease 의 유무를 예측하는 모델이다. (Classification 문제다.)
여하튼 이 Original Dataset 에 Bootstrap 기법을 통해 새로운 Dataset 을 만든다.
Bootstrap 기법은 다른게 아니고, Original Dataset 에서 반복을 허용하여 데이터를 뽑아낸 뒤, Original Dataset 크기의 새로운 Dataset 을 만드는 것이다. 이렇게 만든 Dataset 을 Bootstrapped Dataset 이라 한다.
결과적으로 다음과 같이 만들 수 있다.
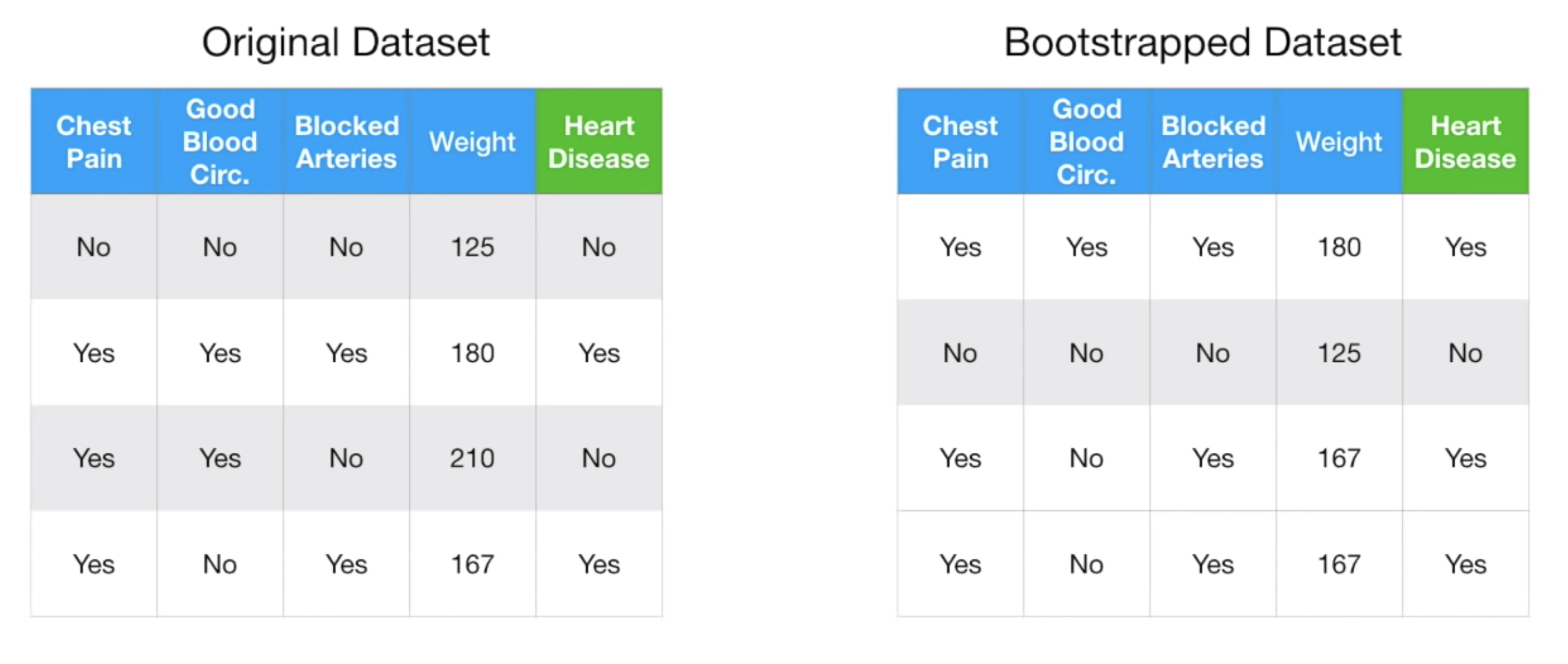
Bootstrapped Dataset 을 보면 3, 4번째 row 의 데이터가 같다. 반복을 허용하여 데이터를 뽑아냈기 때문이다.
아무튼 이 방식으로 Boostrapped Dataset 을 만든다.
2.2. Tree 만들기
이제 이 Boostrapped Dataset 으로 Decsion Tree 를 만들 것이다.
우리가 알고있는 그 Decsion Tree 만드는 방식으로 만들면 된다.
다만, 한 가지 다른 점이 있다.
Decision Tree 에서의 주 이슈는, 어떤 Feature 를 먼저 물어볼 것인가 였다. 즉, 어떤 Feature 가 Tree 의 상단으로 올라가는가 였다.
이 때, 모든 Feature 의 Gini Impurity 를 계산하여, 가장 작은 값을 가지는 Feature 를 먼저 상단으로 올렸다.
그런데, Random Forest 는 모든 Feature 들을 비교하지 않는다. 랜덤하게 일부 Feature 만 골라 Gini Impurity를 비교한다.

Decision Tree 의 방식대로라면, Chest Pain, Good Bllod Circulation, Blocked Arteries, Weight 각각의 Gini Impurity 를 계산했겠지만, 여기서는 랜덤하게 2개를 골랐더니, Good Blood Circulation, Blocked Arteries 가 뽑혔고, 이 2개의 Feature 의 Gini Impurity 만 비교한다.
그 결과, Good Blood Circulation 가 더 낮은 Gini Impurity 를 가졌다고 하자. 따라서 이 Feature 를 Tree 에서 제일 먼저 물어보게 된다.

다음의 과정도 동일하다. 다음을 보자.

다음에 질문해야할 Feature 는 뭘로 두어야할까?
남아있는 Chest Pain, Blocked Arteries, Weight 중, 랜덤하게 2개를 뽑았더니 Chest Pain과 Weight가 뽑혔다.
역시, 이 두 Feature 의 Gini Impurity 를 비교하여 낮은 값을 가지는 Feature 를 Node 로 둔다.
이와 같은 방식으로 아래같이 하나의 Tree 를 완성해나갈 수 있다.
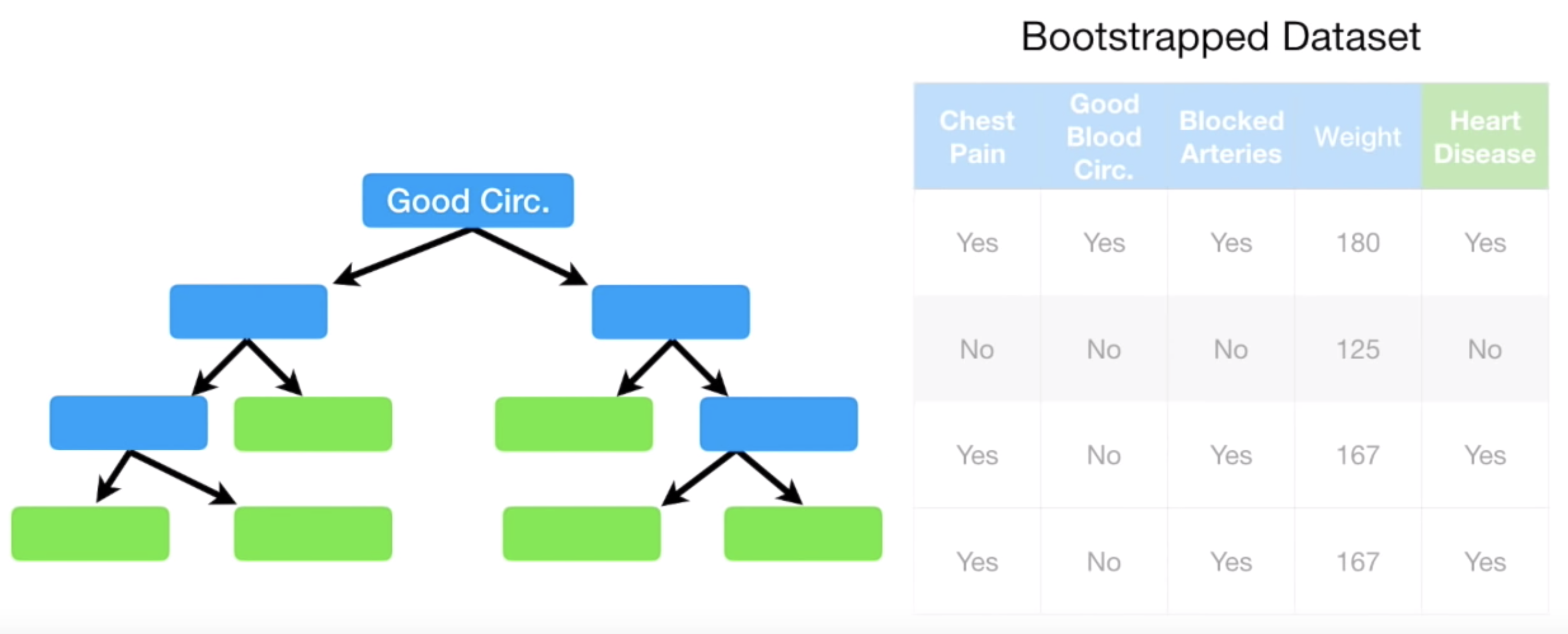
하나가 완성되었으면 다시 Bootstrap Dataset 만드는 과정으로 돌아간다.
다시 Bootstrap 기법으로 새로운 Bootstrap Dataset 을 만들고, 동일한 과정을 통해 또 하나의 Decison Tree 를 만든다.
이렇게 여러번 반복하면, 꽤 많고, 서로 다른 Decsion Tree 를 만들 수 있을 것이다.
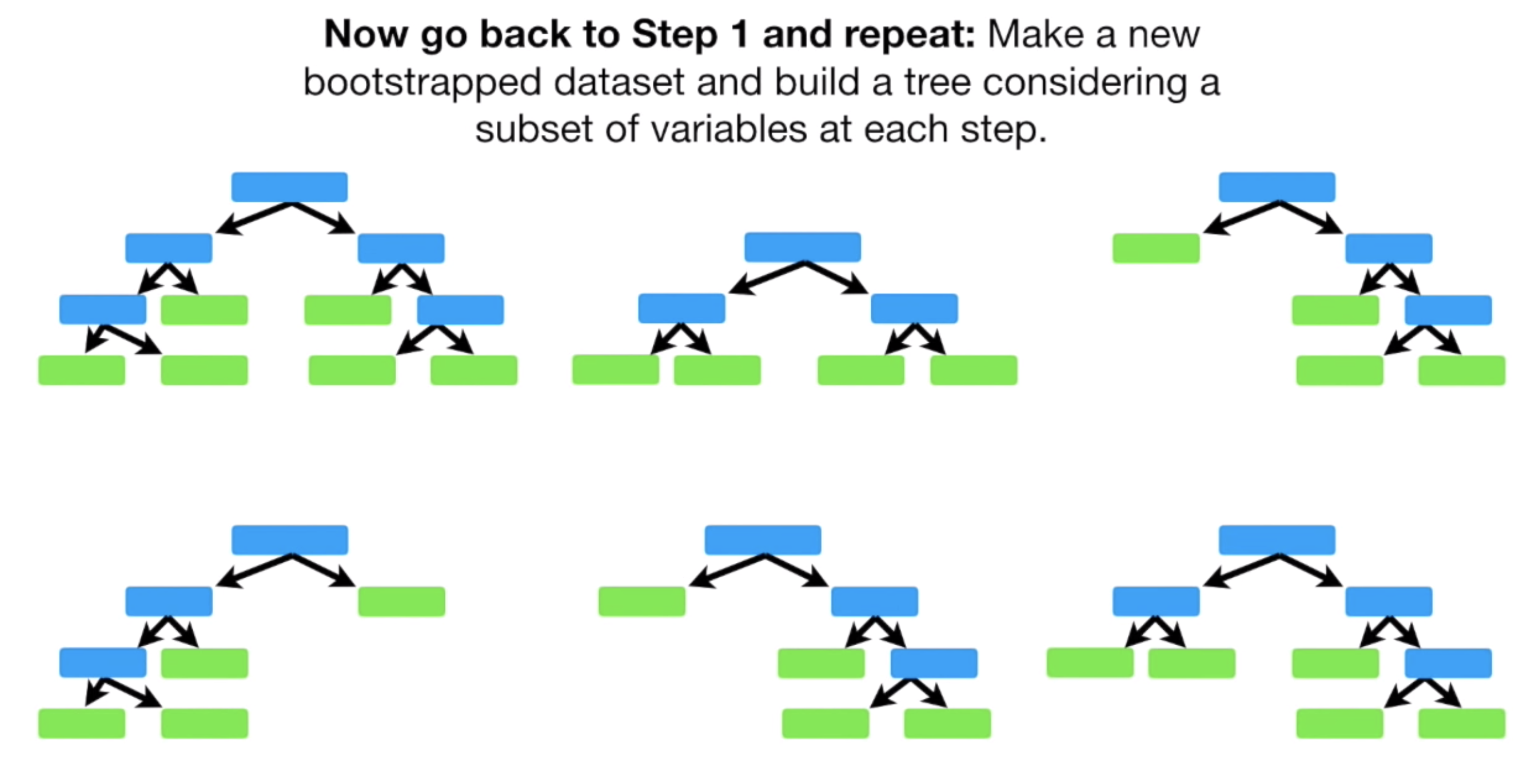
2.3. Voting 하여 최종 결과내기
마지막으로, 데이터를 각각의 Decsion Tree 에 하나씩 넣어 Voting 하여 가장 많이 투표당한 값을 최종값으로 둔다.
예를 들어, 다음과 같은 한명의 환자 데이터가 있다고 하자.
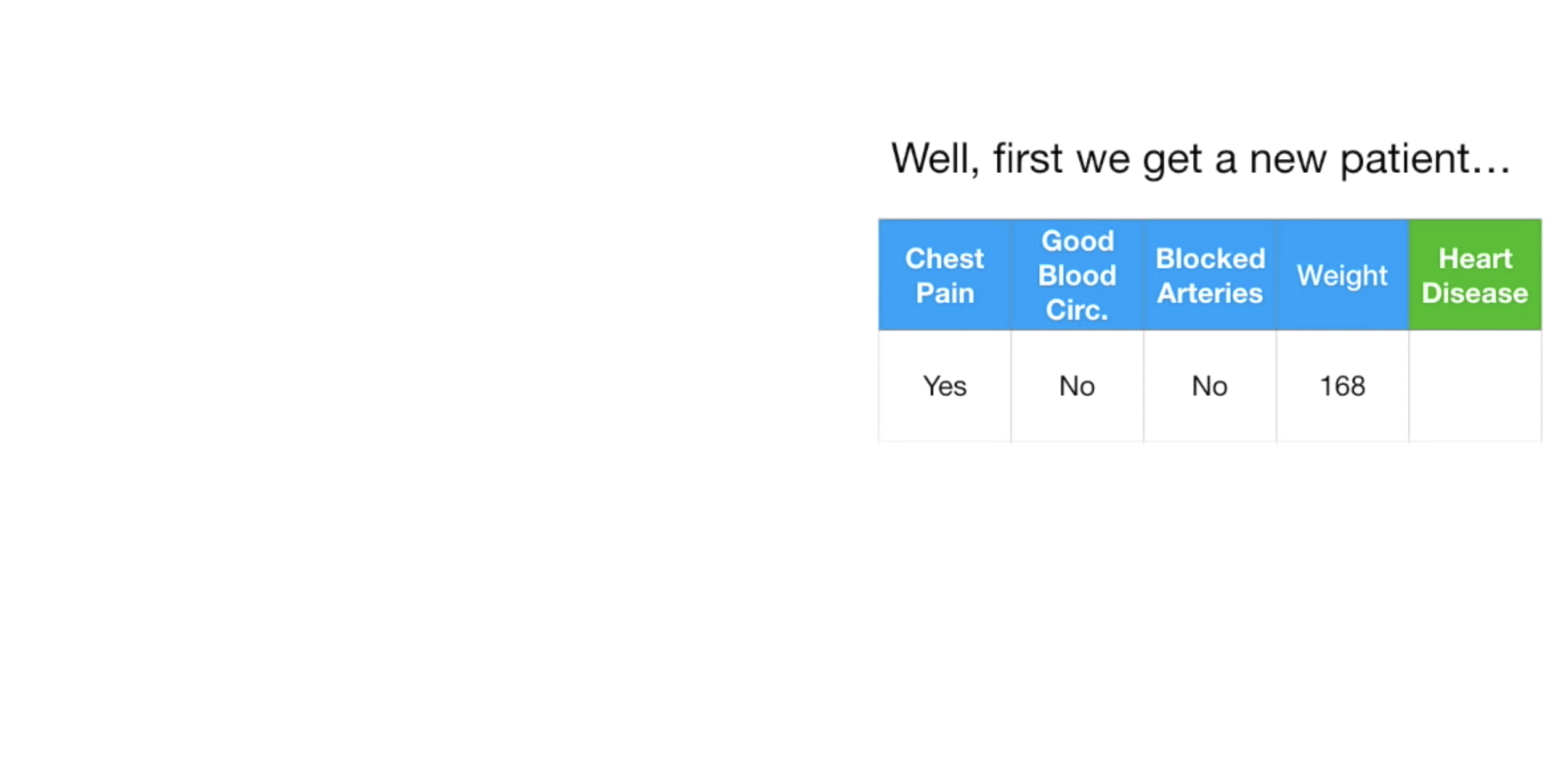
저 데이터를 이제 만들어 놓은 하나의 Decsion Tree 에 넣으면, Tree 상단부터 쭉 내려가 최종적으로 Heart Disease 의 유무를 말해줄 것이다.

이런식으로, 만들어 놓은 모든 Decsion Tree 에 넣으면, 각각의 Tree 마다 Yes 혹은 No 의 값을 출력할 것이다.
이 값들을 Counting 하여, Yes 가 더 많다면 최종적인 값은 Yes 가 되는 것이고, No 가 더 많다면 No 가 되는 것이다.

2.4. 성능 최적화
지금까지 한 방법이 Random Forest 방법이다.
이를 조금 더 최적화 시키는 방법이 있는데, 예를 들어, 랜덤하게 피처를 몇 개 뽑을지를 매번 다르게 하는 방법이다.
위의 예에서는 2개를 랜덤으로 뽑았지만, 3개를 랜덤으로 뽑을 수도 있다.
그럼 2개를 뽑아야 할까? 아니면 3개를 랜덤으로 뽑아야할까?
이건, 2개를 뽑아서도 만들어보고, 3개를 뽑아서도 만들어 본뒤, 성능 체크를 통해 결정하면 된다. 즉 다 해본뒤 좋은걸 뽑으면 된다.
보통의 Random Forest Model 은 이 과정까지 포함한다.
이 외에도, 성능을 최적화 시킬 수 있는 방법들이 더 있을 것이지만, 여기서는 기본적인 과정만 정리해본다.
다시 큰 틀을 보면, 이 모든 과정이 Bagging 의 형태임을 알 수 있다.
- 하나의 Dataset 에서, 여러개의 Dataset 을 만들고
- 각 Dataset 에서 조금은 변형된 Decsion Tree 를 만든다.
- 데이터를 각 Decison Tree 에 입력하고, 나온 예측 값 중, Voting 하여 최종 예측 값을 출력한다.
Random Forest 가 대표적인 Bagging 의 사례임을 이해할 수 있을 것이다.
3. 핵심 키워드
- Bootstrapped Dataset
- Randomly Feature Selecting
- Voting
'데이터와 함께 탱고를 > 머신러닝' 카테고리의 다른 글
| Categorical Value Encoding 과 Mean Encoding (3) | 2019.09.07 |
|---|---|
| Gradient Boost (3) | 2019.08.09 |
| AdaBoost (5) | 2019.08.07 |
| ML Model Ensemble 과 Bagging, Boosting 개념 (1) | 2019.08.07 |
| Decision Tree (1) | 2019.08.05 |
 하나씩 점을 찍어 나가며
하나씩 점을 찍어 나가며


