이 글은 StatQuest with Josh Starmer 의 StatQuest: AdaBoost 영상을 보고 정리한 글이다.
모든 사진과 설명에 대한 출처는 여기에 있다.
이번에는 Boosting 기법에서 대표적이고 비교적 쉬운 개념인 AdaBoost 에 대해 정리해보려고 한다.
항상 Boosting 기법 중 가장 이해하기 쉽기도 하고, 기본 틀이 되는 느낌이라, 가장 먼저 등장하는 것 같다.
하지만 'Boosting 모델 중' 비교적 쉽다는 거지, 이전의 Bagging 모델인 Random Forest 랑 비교하면 조금 복잡하다.
따라서, 글도 매우 길어질 것 같으나... 일단 시작해보겠다.
1. 개념
1.1. Stump
잠깐, Random Forest 를 기억해보면, Random Forest 는 여러 개의 Decison Tree 를 만들 때 다음과 같이 항상 Full size tree 를 만들었다.

Ada Boost 도 시작은 Random Forest 와 비슷하다.
여러개의 Tree 비슷한걸 만드는데, 중요한건 바로 Leaf Node 만 가지는 Tree 를 여러개 만든다.
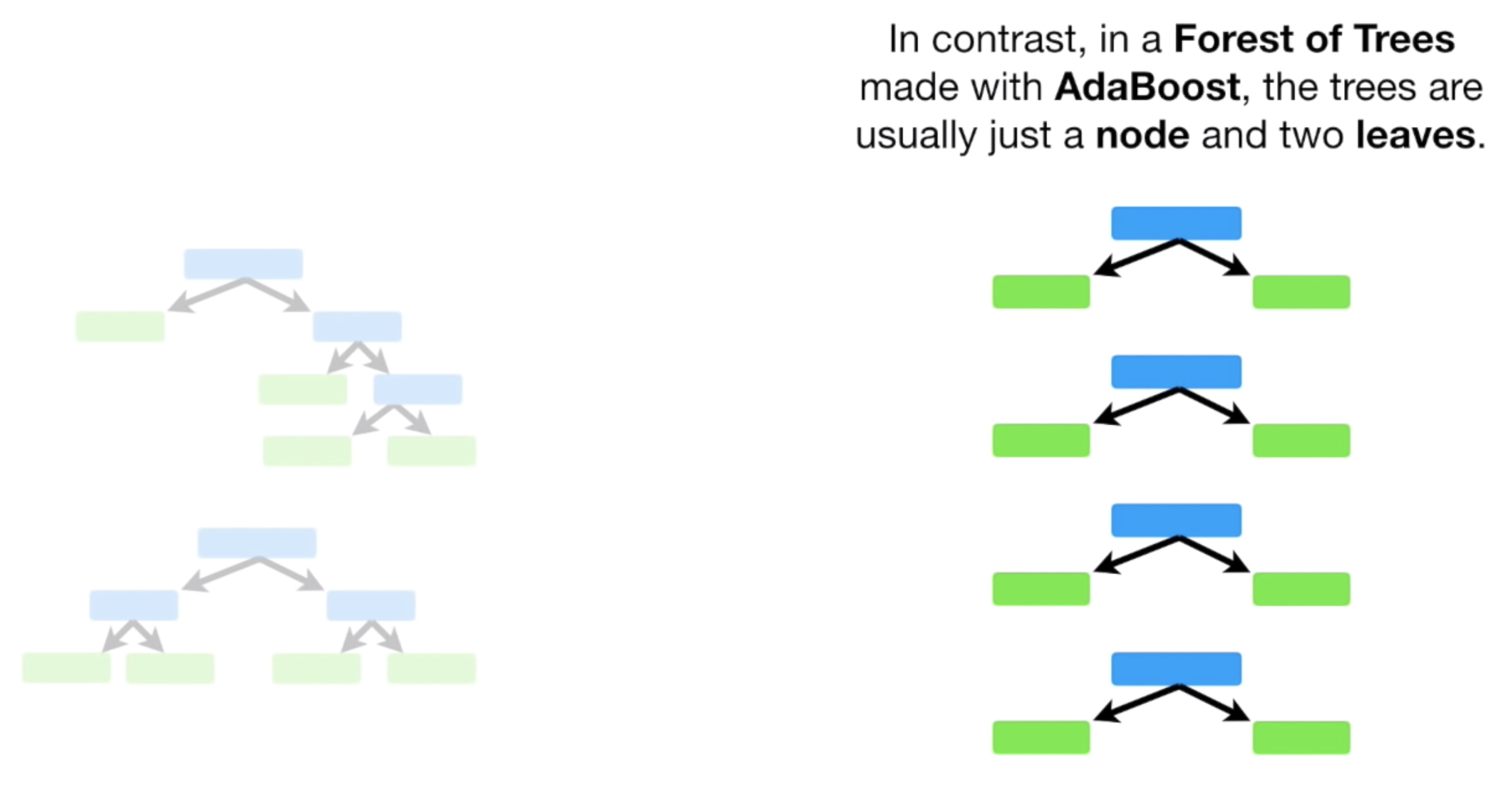
즉, 각 Feature 를 Node 로 두고, Leaf Node 를 바로 가지는 형태로 Tree 비슷한 걸 만든다는 것이다.
이 때, 이런 형태를 Tree 라고 하지않고, Stump 라고 부른다.
Stump 는 데이터의 Feature 수 만큼 생길 것이다.
AdaBoost 는 이러한 Stump 들로 데이터를 예측한다.
하나의 Stump 에다가 데이터를 입력한다고 생각해보자. 너무나 당연하게도, 예측을 잘 못할 것이다.
Decison Tree 나 Random Forest 는 여러번 질문하는 경우지만, Stump 는 한 번만 질문하고 바로 답을 내는 경우니까 말이다.
AdaBoost 는 Stump 를 순차적으로 사용하게 되는데, 순차적으로 데이터를 예측할수록 점점 더 '잘' 예측하게 된다.
이게 Boosting 의 기본 개념이자, AdaBoost 가 앞으로 할 일이다.
과정 파트에서, 제대로 다뤄보도록 하겠다.
1.2. Sample Weight
AdaBoost 부터는 데이터에 Sample Weight 라는 개념이 새로 등장한다.
데이터를 샘플링할 때 각 데이터의 가중치 정도로 해석할 수 있는데, 그냥 직관적으로 설명하면 다음과 같다.

왼쪽과 같은 데이터셋 (이전에도 설명을 많이했으므로 여기서는 데이터에 관한 설명은 생략한다.) 이 있을 때,
최초의 Sample Weight = 1 / 전체 데이터 수 로 정의한다.
그리고, Stump 를 순차적으로 사용할수록 이 Sample Weight 값은 바뀌게 되는데,
한 마디로 설명하자면, 현재 모델에 예측을 잘못한 데이터일수록 Sample Weight 값이 커진다.
이 역시, 과정 파트에서 본격적으로 다뤄보겠다.
2. 과정
이제 실제로, AdaBoost 가 어떻게 작동하는지 살펴보자.
2.1. Stump 고르기
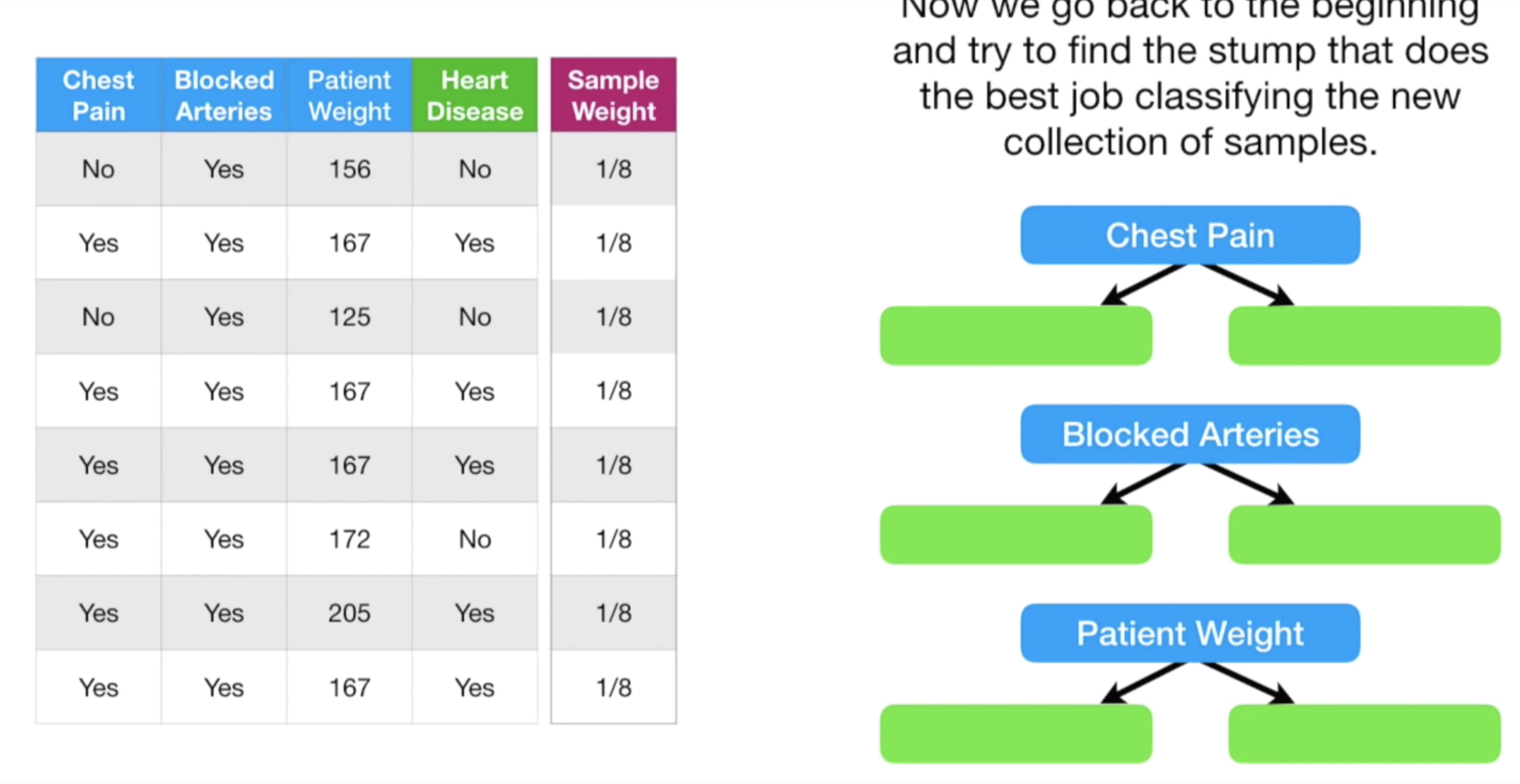
자 먼저, 데이터의 Feature로 Chest Paim, Blocked Arteries, Patient Weight 이 있었다. (위 스크린 샷 참고)
그럼 3개의 Stump 를 만들 수 있으며, 각 Stump 의 Gini Impurity 를 계산할 수 있다.
계산해보니, 이중 Patient Weight Stump 가 Gini Impurity 가 가장 작았다.

따라서, 이 Patient Weight 가 첫 번째로 사용할 Stump 가 된다.
2.2. Sample Weight 업데이트
이제, 우리가 이 Stump 로 예측했을 때, 잘 예측하지 못한 '오류' 에 좀 더 관심을 가져보자.
Leaf Node 에 Incorrect 를 보면, 현재 이 모델(Stump 하나) 이 몇 개의 오류를 냈는지 알 수있다.

해당 오류를 낸 데이터를 데이터셋에서 살펴보니 아래 그림에서 빨간 박스를 친 데이터 였다.
즉, 키가 176보다 작은가? -> No -> 심장병이 없다! 로 예측하는 모델이었는데,
이렇게 했을 때, 4명은 정말 심장병이 없다는, 옳은 결과를 냈지만, 1명은 심장병이 있었던 것이다. 즉 이 1명의 데이터는 오류를 낸다.

여기서 우리는 이 Stump 의 오류를 수치화 하기위해, Total Error 라는 개념을 정의한다.
다음과 같이 정의한다.
Total Error for stump = sum of sample weight of error datas즉, 해당 Stump 의 Total error 는 오류를 내는 데이터들의 Sample Weight 의 총 합이다.
이 예에서는 1/8 이 되겠다.
자 이제, 반대로, 이 Stump 가 말해줄 수 있는 정보량을 수치화 하기위해, Amount of Say 라는 개념을 정의해보겠다.
Total Error 와 마찬가지로, 정보를 수치화하기 위해 만든 것이다.
다음과 같이 정의한다.

왜 이런 모양을 취했을까?
위 값을 Total Error 에 대한 함수로 보면, 다음과 같은 꼴이다.

먼저, Sample Weight 의 값이 0-1 범위였으므로, 이 중 일부 값들의 합인 Total Error 역시 0-1 사이의 값을 가짐을 알 수 있다.
그리고, Total Error 가 커지면, Amount of Say 값이 작아지고, 반대의 경우 Amount of Say 값이 커지는 것을 알 수 있다.
아까 예를 계속 따라가보자.
Total Error 는 1/8 이였으므로, Amount of Say 를 계산하면 다음과 같다.

즉, 대략적으로 우리는 이 Stump 가 데이터를 0.97만큼 잘 예측한다는 것을 수치적으로 알 수 있다.
이제 이 값으로, 우리는 오류를 일으킨 해당 데이터와 나머지 데이터들의 Sample Weight 를 업데이트 할건데,
먼저 오류를 일으킨 해당 데이터의 경우, 같은 방법으로 업데이트 한다.

여기서 amount of say 가 0.97 이었으므로, 이 값을 넣고 계산하면 다음과 같다.

즉 해당 데이터의 새로운 Sample weight 는 0.33 이다. (0.125 -> 0.33 으로 업데이트)
그렇다면, 오류가 아닌 나머지 데이터들은 어떻게 업데이트 시킬까?
다음과 같이 한다.

즉, amount of say 가 양수가 아니라 음수로 만들어 계산한다.
마저 계산하면,
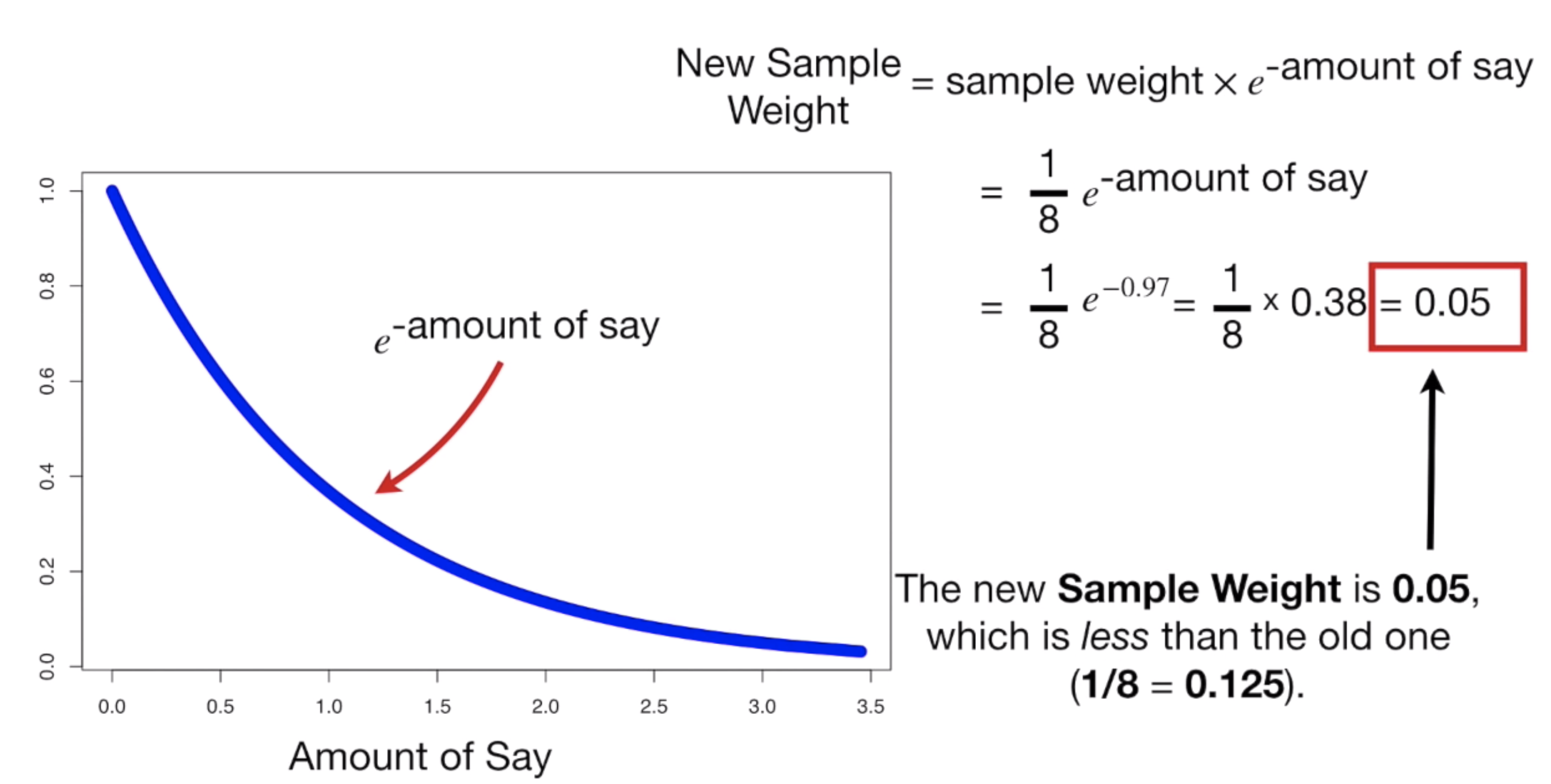
다음과 이 데이터들의 새로운 Sample Weight 값은, 0.05 가 된다. (0.125 -> 0.05 로 변화)
이제, 새로 업데이트된 Sample Weight 를 정리해보면 다음과 같다.

그런데, 이 값들을 모두 더해보면 0.68의 값이 된다.
Sample Weight 은 모두 더해 1이 되게 해야하기 때문에, (애초에 그렇게 정의한 거다.)
이를 0~1 값으로 다시 Normalized 한 값을 써야한다.
이렇게 Normalized 해주면, 0.05 -> 0.07 이 되고, 0.33 -> 0.49가 된다.
이 값들로, Sample Weight 를 업데이트 해준다.

2.3. 다음에 Stump 에 사용할 Dataset 만들기
AdaBoost 는 Stump 들을 하나씩 거쳐가며 점점 더 잘 예측하는 모델을 만드는 거라고 했다.
이제 그 다음 Stump 에 데이터를 넣어야 할텐데, 그 전에 해야할 일이 있다.
바로, 새롭게 업데이트 된 Sample Weight 를 고려하여, 새로운 Dataset 을 만드는 일이다.
새로운 Dataset 은 다음과 같은 방법으로 만든다.
1. 0~1에서 임의의 값을 하나 뽑는다.
2. 뽑힌 값이 0.06 였다. 그럼 기존 Dataset 에서 첫 번째 데이터를 새로운 Dataset에 넣는다.
3. 1을 반복하여 뽑은 값이 0.13 였다. 그럼 기존 Dataset 에서 두 번째 데이터를 새로운 Dataset에 넣는다.
4. 1을 반복하여 뽑은 값이 0.20 였다. 그럼 기존 Dataset 에서 세 번째 데이터를 새로운 Dataset에 넣는다.
5. 1을 반복하여 뽑은 값이 0.31 였다. 그럼 기존 Dataset 에서 세 번째 데이터를 새로운 Dataset에 넣는다.
6. ... 이러한 과정을 새로운 Dataset 이 기존 Dataset 크기가 될 때까지 반복한다.0~1에서 뽑은 값에 따라, 기존 데이터에서 어떤 데이터를 새로운 Dataset 에 넣는지 알겠는가?
- 첫 번째 데이터의 누적 Sample Weight 는 0.07 이었다. 뽑은 값 0.06은 0.07 보다 작으므로, 첫 번째 데이터를 넣는 것이다.
- 두 번째 데이터의 누적 Sample Weight 는 0.14 이다. (0.7 + 0.7). 따라서, 뽑은 값 0.13는 0.14보다 작으므로, 두 번째 데이터를 넣는 것이다.
- 세 번째 데이터의 누적 Sample Weight 는 0.21 이다. (0.7 + 0.7 + 0.7). 따라서, 뽑은 값 0.20는 0.21보다 작으므로, 세 번째 데이터를 넣는 거다.
- 네 번째 데이터의 누적 Sample Weight 는 0.70 이다. (0.7 + 0.7 + 0.7 + 0.49). 따라서, 뽑은 값 0.31는 0.70보다 작으므로, 네 번째 데이터를 넣는 거다.
이런 방식으로 새로운 Dataset 을 만든다.
이렇게하면, Sample Weight 이 큰 데이터들이 새로운 Dataset 에 더 잘 들어가게 된다.
다시 말하면, 오류를 냈던 데이터들이 다음 Stump 에 사용되는 Dataset 으로 더 많이 들어간다는 말이다.
다음 Stump 에서는 이 데이터들이 더 강조될 수 밖에 없다. 그리고 모델은 이 데이터들에 좀 더 fitting 될 것이다.
자연스럽게 Boosting 이 떠오른다. AdaBoost 가 Boosting 기법의 대표적인 이유다.
여하튼 이렇게하면, 다음과 같이 Dataset 이 새로 만들어진다.

그리고 다시, 이 새로운 Dataset 의 Sample Weight 을 데이터마다 동일하게 준다.

그리고 다시 과정의 맨 처음으로 돌아간다.
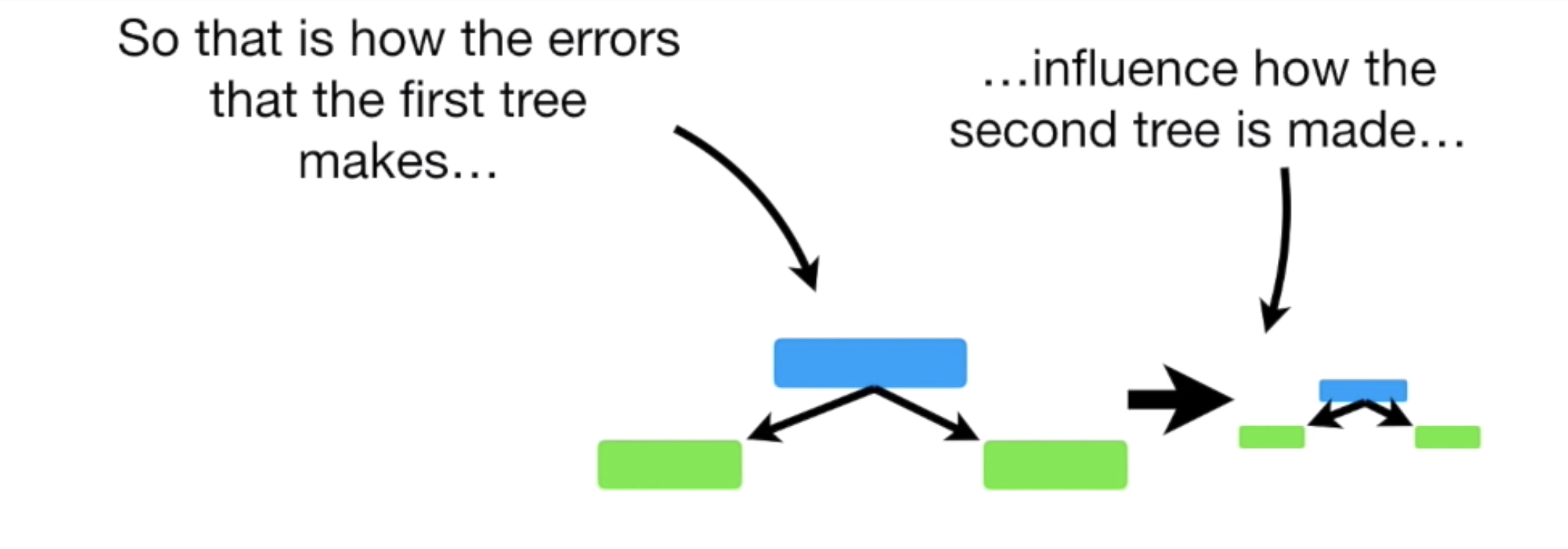
즉, 이 Dataset 을 가지고, Gini Impurity 가 가장 낮은 Stump 를 찾고... 반복 & 반복이다.
이런 방식으로, 첫 번째 Stump 가 다음 Stump 가 예측하는데 영향을 주고.. 그 Stump 는 다음 과정에 영향을 주고... 주고...
이런 과정을 통해 오류를 줄여나가는 것이다.

3. 정리
다시 과정을 정리해보면 다음과 같다.
- Feature 수대로, Stump를 만들고, Gini Impurity 가 낮은 Stump 를 먼저 사용한다.
- 해당 Stump 로 부터 예측한 값 중, 오류들을 고려하여, 기존 Dataset의 Sample Weight 을 업데이트 한다.
- 업데이트 된 Sample Weight 를 고려하여 새로운 Dataset 을 만든다.
- 이 Dataset 으로 1~3을 반복하여, 점점 높은 예측력을 가지는 모델을 만든다.
4. 핵심키워드
- Stump
- Total Error, Amount of say
- Sample Weight
- Boosting
'데이터와 함께 탱고를 > 머신러닝' 카테고리의 다른 글
| Categorical Value Encoding 과 Mean Encoding (3) | 2019.09.07 |
|---|---|
| Gradient Boost (3) | 2019.08.09 |
| Random Forest (2) | 2019.08.07 |
| ML Model Ensemble 과 Bagging, Boosting 개념 (1) | 2019.08.07 |
| Decision Tree (1) | 2019.08.05 |
 하나씩 점을 찍어 나가며
하나씩 점을 찍어 나가며


