머신러닝을 위한 파이썬 워밍업에서 Linear Regression 파트를 공부하며 복습한 내용을 적어본다.
선형회귀 모델은 y = Wx + b 다.
우리는 데이터(x) 를 가지고 어떤 결과(y)를 예측하는 어떤 모델(y=Wx+b) 를 만들려고 한다. 즉 결과적으로 "모델", 을 만드는 것인데, 이 모델은 구체적으로 각 변수에 곱해지는 계수항들의 묶음 W와 상수항인 b를 의미하고, 이 두 변수를 구하는 것이 기계학습의 목표이다.
이를 어떻게 구할까? 에 앞서, 이에 대해 강의에서는 2가지를 설명해주는데, Normal Equation과 Gradient Descent다.
Normal Equation
y = Wx + b 에서 b 는 x 에 [1] 로 구성된 열을 추가해주면, y = Wx + b 를 y = xW' 로 바꿀 수 있다.
지금 여기에서 우리가 구하자고 하는 것은 W' 이다. Normal equation 에 따르면, 수학적으로 W 는 다음과 같이 알려져있다.
X, Y가 주어지면, numpy를 이용해 위 식을 쉽게 코드화 할 수 있다.
이렇게 나온 이유는 다음 링크를 참조하자.
쉬운 Normal Equation의 이해
http://blog.naver.com/PostView.nhn?blogId=skkong89&logNo=220565068304
Gradient Descent
MSE와 Cost function
먼저 랜덤적으로 W와 b가 있다고 하자.
이 모델이 올바른지는 이렇게 해서 구한 y' 와 실제 데이터의 y를 비교해보면 되는데, 다음과 같이 비교할 수 있다.
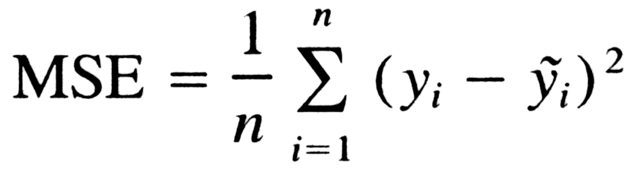
Mean Squared Error 라고 하여 MSE 라고 하는데, 말 그대로 '에러', '오류' 를 나타내는 지표다.
이 값이 낮으면 낮을수록 오류가 적은 것이므로, 올바른 모델이라고 할 수 있다.
Cost function 은 이 MSE 를 그대로 가져온 것인데, 변화하는 W에 따라 y' 이 바뀌고, 결과적으론 MSE 값이 바뀌므로 *W값을 입력으로 주면 에러값을 출력하는 *일종의 함수로 보는 것이다. 일반적인 cost function J 식은 아래와 같다.
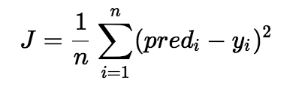
에러가 적을수록 좋은 모델이라 할 수 있으므로, Cost function의 값이 0에 가깝게 하는 W값을 찾아야 한다.
이 함수가 어떻게 생겼는지 조차 모르는데, 어떻게 최소값인 W 지점을 찾을 수 있을까?
Gradient Descent
Gradient Descent 는 이 Cost function을 이용하여 W를 찾아가는 기발한 방법이다.
위에서 말했듯, 우리는 일반적으로 이 함수의 생김새를 모른다. 우리가 함수에서 현재 어떤 지점 θ 에 있다고 하자. 이 θ 에서 조금씩 조금씩 움직이며 최소값이 되는 부분을 찾아 나갈 수 있다.
그럼 얼마만큼 움직일 것인가? 현재 cost function J(θ) 을 미분하고 거기에 일정 상수 a를 곱한 만큼 움직인다.
이 과정을 계속해서 진행한다. 식으로 보면 다음과 같다.
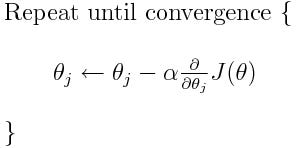
진행하다가, θ가 극소점에 오게되었을 때, cost function 의 미분값은 0에 가까워지게 된다. (고등학교 때 배운 극대 극소점 찾는 방법이다.) 따라서, 극소점에 다다랐을 때, θ는 더 이상 업데이트 되지 않고 한 점에 머무르게 된다. 이 점이 우리가 찾던 올바른 W 값이 된다.
Full Batch Gradient Descent
굳이굳이 구분하면, 1개 데이터를 가지고 미분하여 W를 찾아내는 것을 Gradient Descent 라고 하고,
여러개의 데이터를 다 미분하여 미분값의 평균으로 W를 찾아내는 것을 Full Batch Gradient Descent라고 한다.
즉, 한 데이터냐, 전체 데이터냐에 따라 Batch의 이름이 붙는 것이고, 하나와 전체 중간 정도의 데이터를 쓴다면 Mini Batch 라는 이름이 붙는다.
위에선 굳이굳이 나누었지만 일반적으로 GD(Gradient Descent) 라고 하면 Full Batch Gradient Decent를 의미한다.
위에서 cost function J의 식만 보더라도 n개의 데이터에 대해 제곱합을 구한 후, 평균을 내는 것을 볼 수 있는데, 이 식을 이용하여, GD를 진행하면 Full Batch GD를 하는 것이다.
Stochastic Gradient Descent
이전 GD에서 cost fuction J에 들어오는 x값은 사실 데이터의 연속된 x값을 가진 데이터라고 가정하고 있다. 데이터의 형태가 (x, y) 라고 할 때, X = [ (1, 2), (2, 3), (5, 4), (6, 5) ] 식으로, x 값이 1, 2, 5, 6 처럼 연속적인 형태다.
따라서 GD로 데이터의 x값을 따라 하나씩 탐색한다고 할 때, 그래프에서 어떤 연속된 구간에서 극소점을 향해 탐색해나가는 꼴인 것이다. 이 방식이면, 전체 그래프의 극소점이 아니라, 한 구간의 극소점에만 도달할 여지가 있다. 그래서 연속된 x값을 탐색하는게 아니라, x값을 미리 셔플한 뒤, 로컬적으로 연속된 구간이 아니라 좀 더 글로벌하게 탐색하게 할 수 있는데 이 방법이 Stochastic GD (SGD) 다.
SGD로 하면 X = [ (2, 3), (5, 4), (1,2), (6, 5) ] 로 이전과 달리 데이터 값들이 섞이게 된다. 직관적으로 일반 GD와 SGD의 차이는 이 X값을 셔플해주냐 안해주느냐의 차이다.
Mini Batch Stochastic Gradient Descent
위 SGD 방식에 Mini Batch 방식을 더하면 Mini Batch Stochastic Gradient Descent 이 된다.
하나의 데이터로만 W 값을 찾기 좀 뭐하고, 모든 데이터로 다 하자고 하니, 시간이 너무 오래걸리고.. 그냥 GD로 하기엔 로컬 극소점을 찾는 문제의 여지가 있으니, 이 모든걸 고려한게 이 방법이다. 그래서 일반적으로 제일 많이 쓰는 GD 기법이라고 한다.
정리
강의 PT에서 비교 사진 일부를 넣어 정리해보겠다.
아래 사진은 4가지 방식 (GD, Full GD, SGD, MBSGD) 가 어떻게 다른지 보여준다.

아래는 구현하는 수도 코드이다.
함수의 각 파라미터들의 차이를 보면 4개가 어떻게 다른지 한 눈에 볼 수 있다.

참고하면 좋은 링크
Difference between Batch Gradient Descent and Stochastic Gradient Descent
'데이터와 함께 탱고를 > 통계 기초 공부' 카테고리의 다른 글
| 두 집단의 평균차이에 대한 가설 검정 (1) | 2019.04.22 |
|---|---|
| 가설검정 단계 (지금까지) (0) | 2019.04.18 |
| 표본 분산은 왜 n-1로 나눌까? (0) | 2019.04.18 |
| L1, L2 Regularization (Lasso, Ridge) (0) | 2019.04.09 |
| 헷갈리는 .reshape 과 broadcasting (3) | 2019.04.04 |
 하나씩 점을 찍어 나가며
하나씩 점을 찍어 나가며


